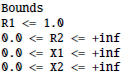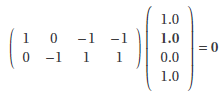Difference between revisions of "Flux Balance Constraint (analysis)"
(Space after icon) |
(Plugin name added) |
||
| Line 3: | Line 3: | ||
;Provider | ;Provider | ||
:[[Institute of Systems Biology]] | :[[Institute of Systems Biology]] | ||
| + | ;Plugin | ||
| + | :biouml.plugins.fbc (Flux Balance) | ||
=== Flux balance Analysis === | === Flux balance Analysis === | ||
Revision as of 11:47, 6 May 2013
- Analysis title
 Flux Balance Constraint
Flux Balance Constraint
- Provider
- Institute of Systems Biology
- Plugin
- biouml.plugins.fbc (Flux Balance)
Flux balance Analysis
Flux balance analysis is a mathematical approach for analyzing the flow of metabolites through a metabolic network.
Metabolic reactions are represented as a stoichiometric matrix S. The flux through all of the reactions in a network is represented by the vector v. Flux Balance Analysis seeks to maximize or minimize an objective function Z = cTv, which can be any linear combination of fluxes, where c is a vector of weights, indicating how much each reaction contributes to the objective function. FBA can thus be defined as the use of linear programming to solve the equation Sv = 0 given a set of upper and lower bounds on v and a linear combination of fluxes as an objective function.
Parameters:
- Diagram path – Path to input diagram
- Data Table Path – Path to FBC data table
- Result path – Path to resulting element
- Type Objective Function (expert) – TypeObjectiveFunction
Example
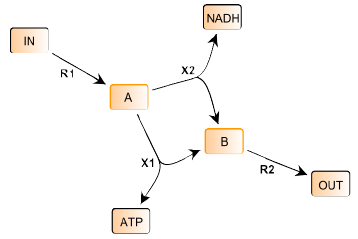
FBC syntax example: a simple four reaction pathway. The reactions are R1, R2, X1, X2 with fixed species IN, OUT, ATP, NADH and variable species A, B.
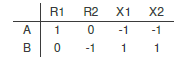
Using the reagent identity and stoichiometry it is possible to compactly describe this network in terms of its reaction stoichiometry:
There are capacity constraints in this example:
In this example the flux through reaction R2 will be maximized. Solving this we find that maximization of flux through R2 gives an optimal solution R2 = 1 with one possible solution for v.
- Jeffrey D. Orth, Ines Thiele and Bernhard O. Palsson, "What is flux balance analysis?". Nature Biotechnology 28, 245–248 2010.
- SBML Level 3 Package Specification