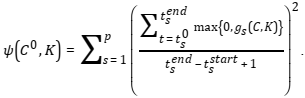Difference between revisions of "Optimization problem"
(Created page with "The general nonlinear optimization problem [1] can be formulated as follows: find a minimum of the objective function ϕ(''x''), where ''x'' lies in the intersection of the ''...") |
|||
| (44 intermediate revisions by one user not shown) | |||
| Line 8: | Line 8: | ||
[[File:optimization_formula_2.png]] | [[File:optimization_formula_2.png]] | ||
| + | In order to get solution situated inside ℱ, we minimize the penalty function | ||
| + | [[File:optimization_formula_3.png]] | ||
| + | |||
| + | The problem could be solved by different optimization methods. We implemented the following of them in the [[BioUML]] software: | ||
| + | |||
| + | <ul> | ||
| + | <li>stochastic ranking evolution strategy (SRES) [1];</li> | ||
| + | <li>cellular genetic algorithm MOCell [2];</li> | ||
| + | <li>particle swarm optimization (PSO) [3];</li> | ||
| + | <li>deterministic method of global optimization glbSolve [4];</li> | ||
| + | <li>adaptive simulated annealing (ASA) [5].</li> | ||
| + | </ul> | ||
| + | |||
| + | The below table shows the generic scheme of the optimization process for these methods. SRES, MOCell, PSO and glbSolve run a predefined number of iterations ''N<sub>it</sub>'' considering a sequence of sets (populations) ''P<sup>i</sup>'', ''i'' = 0,…,''N<sub>it</sub>'' − 1, of potential solutions (guesses). In the case of the first three methods, the size ''s'' ∈ ℕ<sup>+</sup> of the population is fixed, whereas in glbSolve the initial population ''P''<sup>0</sup> consists of one guess, while the size ''s''<sub>''k''+ 1</sub> of the population ''P''<sup>''k''+1</sup> is found during the iteration | ||
| + | with the number ''k'' = 0,…, ''N<sub>it</sub>'' − 1. The method ASA considers sequentially generated guesses ''x<sup>k</sup>'' ∈ Ω, ''k'' ∈ ℕ<sup>+</sup>, and stops if distance between ''x<sup>k</sup>'' and ''x''<sup>''k''+1</sup> defined as Euclidean norm | ||
| + | |||
| + | [[File:optimization_formula_4.png]] | ||
| + | |||
| + | becomes less than a predefined accuracy ε. | ||
| + | |||
| + | [[File:optimization_table_1.png]] | ||
| + | |||
| + | All methods, excepting glbSolve, are stochastic and seek global minimum of the function ϕ taking into account the admissible region ℱ. Thus, a guess ''x'' ∈ Ω is more preferable than a guess ''y'' ∈ Ω at some iteration of methods, if ψ(''x'') = 0 and ψ(''y'') ≠ 0 or ψ(''x'') < ψ(''y''). The method glbSolve is suited to solve only the problems with Ω ⊆ ℱ. Values of the function ψ are calculated but do not affect on the generation of potential solutions. | ||
| + | |||
| + | ==Application of non-linear optimization to systems biology== | ||
| + | |||
| + | We assume that a mathematical model of some biological process consists of a set of chemical species ''S'' = {''S''<sub>1</sub>,…,''S<sub>m</sub>''} associated with variables ''C''(''t'') = (''C''<sub>1</sub>(''t''),…,''C<sub>m</sub>''(''t'')) representing their concentrations, and a set of biochemical reactions ℛ = {''R''<sub>1</sub>,…,''R<sub>n</sub>''} with rates ''v''(''t'') = (''v''<sub>1</sub>(''t''),…,''v<sub>n</sub>''(''t'')) depending on a set of kinetic constants ''K''. Reaction rates are modeled by standard laws of chemical kinetics. A Cauchy problem for ordinary differential equations representing a linear combination of reaction rates is used to describe the model behavior over time: | ||
| + | |||
| + | [[File:optimization_formula_5.png]]   '''(*)''' | ||
| + | |||
| + | Here ''N'' is a stoichiometric matrix of ''n'' by ''m''. We say that ''C<sup>ss</sup>'' is a steady state of the system '''(*)''' if | ||
| + | |||
| + | [[File:optimization_formula_6.png]] | ||
| + | |||
| + | Identification of parameters ''K'' and initial concentrations ''C''<sup>0</sup> is based on experimental data represented by a set of points ''C<sub>i</sub><sup>exp</sup>''(''t<sub>i,j</sub>'') defining dynamics of variables ''C''<sub>1</sub>(''t''),…,''C<sub>l</sub>''(''t''), ''l'' ≤ ''m'', at given times ''t<sub>i,j</sub>'', ''j'' = 1,…,''r<sub>i</sub>'', where ''r<sub>i</sub>'' is the number of | ||
| + | such points for the concentration ''C<sub>i</sub>''(''t''), ''i'' = 1,…,''l''. The problem of parameter identification consists in minimization of the function of deviations defined as the normalized sum of squares [6]: | ||
| + | |||
| + | [[File:optimization_formula_7.png]] | ||
| + | |||
| + | where normalization factors ω<sub>min</sub>/ω<sub>''i''</sub> with ω<sub>min</sub> = min<sub>''i''</sub>ω<sub>''i''</sub> are used to make all concentration trajectories have similar | ||
| + | importance. The weights ω<sub>''i''</sub> are calculated by one of the formulas on experimentally measured concentrations: | ||
| + | |||
| + | [[File:optimization_formula_8.png]] (mean square value), [[File:optimization_formula_9.png]] (mean value), [[File:optimization_formula_10.png]] (standard deviation). | ||
| + | |||
| + | If we want to consider additional constrains | ||
| + | |||
| + | [[File:optimization_formula_11.png]] | ||
| + | |||
| + | holding for concentrations ''C''(''t'') and parameters ''K'' for some period of time [[File:optimization_formula_12.png]], the penalty function is defined as | ||
| + | |||
| + | [[File:optimization_formula_13.png]] | ||
| + | |||
| + | This function assumes summation of values ''g<sub>s</sub>''(''C'',''K'') in the nodes of grid defined by an ODE solver to find a numerical | ||
| + | solution of the system '''(*)'''. | ||
| + | |||
| + | In the particular case, experimental data could be represented by steady state values of species concentrations. Then functions ϕ and ψ have the simpler forms: | ||
| + | |||
| + | [[File:optimization_formula_14.png]] | ||
| + | |||
| + | where ''C<sub>i</sub><sup>exp_ss</sup>'' and ''C<sub>i</sub><sup>ss</sup>'', ''i'' = 1,…,''l'', denote experimental and simulated steady state values. | ||
| + | |||
| + | Typically, researchers want to perform evaluation of model parameters using experimental data obtained with different | ||
| + | experimental conditions, i.e. different initial concentrations ''C''<sup>01</sup>,…,''C''<sup>0''k''</sup> of species. In such case, we will consider the functions | ||
| + | |||
| + | [[File:optimization_formula_15.png]] | ||
| + | |||
| + | ==Implementation of the parameter estimation process in BioUML== | ||
| + | |||
| + | [[BioUML]] allows performing parameter estimation by creation a special optimization document. For details about this document, see the section [[Optimization document]]. | ||
| + | Examples of the BioUML application for solving optimization problems is done in the section [[Optimization examples]]. You can also found more details in the article [7]. | ||
==References== | ==References== | ||
| − | # Runarsson T.P., Yao X. Stochastic ranking for constrained evolutionary optimization. ''IEEE Transactions on Evolutionary Computation''. 2000. 4(3):284–294 | + | # Runarsson T.P., Yao X. Stochastic ranking for constrained evolutionary optimization. ''IEEE Transactions on Evolutionary Computation''. 2000. 4(3):284–294. |
| + | # Nebro A.J., Durillo J.J., Luna F., Dorronsoro B., Alba E. MOCell: A cellular genetic algorithm for multiobjective optimization. ''International Journal of Intelligent Systems''. 2009. 24(7):726–746. | ||
| + | # Sierra M.R., Coello C.A. Improving PSO-Based Multi-objective Optimization Using Crowding, Mutation and ∈-Dominance. ''Evolutionary Multi-Criterion Optimization''. ''Lecture Notes in Computer Scienc''. 2005. 3410:505-519. | ||
| + | # Björkman M., Holmström K. Global Optimization Using the DIRECT Algorithm in Matlab. ''Advanced Modeling and Optimization''. 1999. 1(2):17–37. | ||
| + | # Ingber L. Adaptive simulated annealing (ASA): Lessons learned. ''Control and Cybernetics''. 1996. 25(1):33–54. | ||
| + | # Hoops S., Sahle S., Gauges R., Lee C., Pahle J., Simus N., Singhal M., Xu L., Mendes P., Kummer U. COPASI-a COmplex PAthway SImulator. ''Bioinformatics''. 2006. 22(24):3067–3074. | ||
| + | # Kutumova E., Ryabova A., Valeev T., Kolpakov F. BioUML plug-in for nonlinear parameter estimation using multiple experimental data. ''Virtual biology''. 2013. 1:47-58. | ||
Latest revision as of 13:30, 3 September 2021
The general nonlinear optimization problem [1] can be formulated as follows: find a minimum of the objective function ϕ(x), where x lies in the intersection of the N-dimensional search space
and the admissible region ℱ ⊆ ℝN defined by a set of equality and/or inequality constraints on x. Since the equality gs(x) = 0 can be replaced by two inequalities gs(x) ≤ 0 and –gs(x) ≤ 0, the admissible region can be defined without loss of generality as
In order to get solution situated inside ℱ, we minimize the penalty function
The problem could be solved by different optimization methods. We implemented the following of them in the BioUML software:
- stochastic ranking evolution strategy (SRES) [1];
- cellular genetic algorithm MOCell [2];
- particle swarm optimization (PSO) [3];
- deterministic method of global optimization glbSolve [4];
- adaptive simulated annealing (ASA) [5].
The below table shows the generic scheme of the optimization process for these methods. SRES, MOCell, PSO and glbSolve run a predefined number of iterations Nit considering a sequence of sets (populations) Pi, i = 0,…,Nit − 1, of potential solutions (guesses). In the case of the first three methods, the size s ∈ ℕ+ of the population is fixed, whereas in glbSolve the initial population P0 consists of one guess, while the size sk+ 1 of the population Pk+1 is found during the iteration with the number k = 0,…, Nit − 1. The method ASA considers sequentially generated guesses xk ∈ Ω, k ∈ ℕ+, and stops if distance between xk and xk+1 defined as Euclidean norm
becomes less than a predefined accuracy ε.
All methods, excepting glbSolve, are stochastic and seek global minimum of the function ϕ taking into account the admissible region ℱ. Thus, a guess x ∈ Ω is more preferable than a guess y ∈ Ω at some iteration of methods, if ψ(x) = 0 and ψ(y) ≠ 0 or ψ(x) < ψ(y). The method glbSolve is suited to solve only the problems with Ω ⊆ ℱ. Values of the function ψ are calculated but do not affect on the generation of potential solutions.
[edit] Application of non-linear optimization to systems biology
We assume that a mathematical model of some biological process consists of a set of chemical species S = {S1,…,Sm} associated with variables C(t) = (C1(t),…,Cm(t)) representing their concentrations, and a set of biochemical reactions ℛ = {R1,…,Rn} with rates v(t) = (v1(t),…,vn(t)) depending on a set of kinetic constants K. Reaction rates are modeled by standard laws of chemical kinetics. A Cauchy problem for ordinary differential equations representing a linear combination of reaction rates is used to describe the model behavior over time:
Here N is a stoichiometric matrix of n by m. We say that Css is a steady state of the system (*) if
Identification of parameters K and initial concentrations C0 is based on experimental data represented by a set of points Ciexp(ti,j) defining dynamics of variables C1(t),…,Cl(t), l ≤ m, at given times ti,j, j = 1,…,ri, where ri is the number of such points for the concentration Ci(t), i = 1,…,l. The problem of parameter identification consists in minimization of the function of deviations defined as the normalized sum of squares [6]:
where normalization factors ωmin/ωi with ωmin = miniωi are used to make all concentration trajectories have similar importance. The weights ωi are calculated by one of the formulas on experimentally measured concentrations:
![]() (mean square value),
(mean square value), ![]() (mean value),
(mean value), ![]() (standard deviation).
(standard deviation).
If we want to consider additional constrains
holding for concentrations C(t) and parameters K for some period of time ![]() , the penalty function is defined as
, the penalty function is defined as
This function assumes summation of values gs(C,K) in the nodes of grid defined by an ODE solver to find a numerical solution of the system (*).
In the particular case, experimental data could be represented by steady state values of species concentrations. Then functions ϕ and ψ have the simpler forms:
where Ciexp_ss and Ciss, i = 1,…,l, denote experimental and simulated steady state values.
Typically, researchers want to perform evaluation of model parameters using experimental data obtained with different experimental conditions, i.e. different initial concentrations C01,…,C0k of species. In such case, we will consider the functions
[edit] Implementation of the parameter estimation process in BioUML
BioUML allows performing parameter estimation by creation a special optimization document. For details about this document, see the section Optimization document. Examples of the BioUML application for solving optimization problems is done in the section Optimization examples. You can also found more details in the article [7].
[edit] References
- Runarsson T.P., Yao X. Stochastic ranking for constrained evolutionary optimization. IEEE Transactions on Evolutionary Computation. 2000. 4(3):284–294.
- Nebro A.J., Durillo J.J., Luna F., Dorronsoro B., Alba E. MOCell: A cellular genetic algorithm for multiobjective optimization. International Journal of Intelligent Systems. 2009. 24(7):726–746.
- Sierra M.R., Coello C.A. Improving PSO-Based Multi-objective Optimization Using Crowding, Mutation and ∈-Dominance. Evolutionary Multi-Criterion Optimization. Lecture Notes in Computer Scienc. 2005. 3410:505-519.
- Björkman M., Holmström K. Global Optimization Using the DIRECT Algorithm in Matlab. Advanced Modeling and Optimization. 1999. 1(2):17–37.
- Ingber L. Adaptive simulated annealing (ASA): Lessons learned. Control and Cybernetics. 1996. 25(1):33–54.
- Hoops S., Sahle S., Gauges R., Lee C., Pahle J., Simus N., Singhal M., Xu L., Mendes P., Kummer U. COPASI-a COmplex PAthway SImulator. Bioinformatics. 2006. 22(24):3067–3074.
- Kutumova E., Ryabova A., Valeev T., Kolpakov F. BioUML plug-in for nonlinear parameter estimation using multiple experimental data. Virtual biology. 2013. 1:47-58.