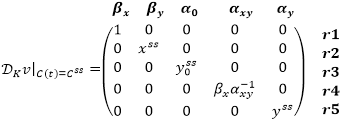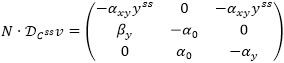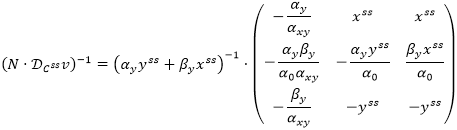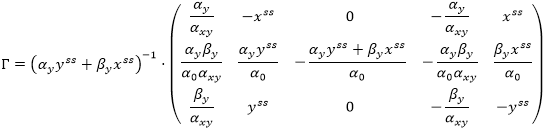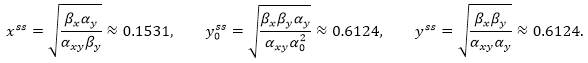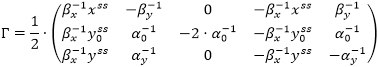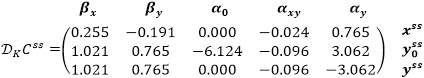Difference between revisions of "Metabolic control analysis example"

Revision as of 16:52, 11 March 2022

The method description could be found in the section Metabolic Control Analysis. Here we give an example of the method application and using in BioUML.

Reproducing a test case in BioUML

To reproduce a test case below in the BioUML workbench, go to the Analysis tab in the navigation pane and follow to analyses > Methods > Differential algebraic equations.

After double click on Metabolic Control Analysis, a new tab with analysis settings opens.

Select a path to an example input diagram:

data/Examples/DAE models/Data/Diagrams/Geva_Zatorsky_2006_Model_I

and a path to save results of analysis, for example:

data/Collaboration/Demo/Data/Temp/Metabolic Control Analysis

After you click the Run button and the calculations are finished, you can see the results presented in six tables, including unscaled elastisities (the matrix Ɗ_C^ssv in the description below), unscaled concentration controls (the matrix Γ), unscaled flux controls (the matrix Λ), and scaled versions of these matrices with elements e_i,j defined as a product of the corresponding elements in the unscaled matrixes and values of c_i,j / r_i,j, where c_i,j and r_i,j denote steady state values of column and row elements, respectively.

Ready analysis results can be found here:

data/Examples/DAE models/Data/Metabolic Control Analysis

Description of the test case

The theory of metabolic control determines sensitivity of steady metabolic fluxes (reaction rates) v^ss and steady state C^ss of an ODE model under perturbation of its parameters K [1]. Unlike the Sensitivity Analysis, this method does not require the computation of values C^ss(p + Δp), p ∈ K, that can accelerate the model research. Instead, to analyze matrixes Ɗ_KC^ss and Ɗ_Kv^ss of partial derivatives of C^ss and v^ss with respect to parameters K, the method considers a matrix Ɗ_Kv|_{C(t) = C^ss} of partial derivatives of a vector v(t) with respect to K in a steady state of the model, and searches for control matrices Γ and Λ, such that

In accordance with [1], these matrices can be calculated by formulas

where N_R is a matrix consisting of linearly independent rows of the model stoichiometric matrix N of n by m, L is a transition matrix such that: N = L · N_R, and Ɗ_C^ssv is a matrix of elasticity coefficients

.

Consider the model of p53 and Mdm2 proteins regulation described in the example for Sensitivity Analysis. For this model, we get:

Next, we find the matrixes N and Ɗ_C^ssv:

Since N_R = N and L is the identity matrix of 3 by 3, we can calculate the matrix product N · Ɗ_C^ssv:

Applying the cofactor method to the resulting matrix, we deduce:

Thus, we have:

Take into account the formulas for calculation of the model steady state derived in the Sensitivity Analysis example:

Using these formulas, we can convert matrix Γ to the form:

Multiplication of the calculated matrices Γ and Ɗ_Kv|_{C(t) = C^ss} gives the same matrix Ɗ_KC^ss, as in the example for Sensitivity Analysis:

References

1. Reder C. Metabolic control theory: a structural approach. Journal of Theoretical Biology. 1988. V. 135. № 2. p. 175-201.