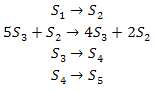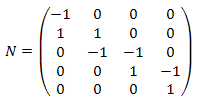Difference between revisions of "Stoichiometric Matrix (analysis)"
(Plugin name added) |
(Automatic synchronization with BioUML) |
||
| (6 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
;Analysis title | ;Analysis title | ||
| − | :[[File: | + | :[[File:Default-analysis-icon.png]] Stoichiometric Matrix |
;Provider | ;Provider | ||
:[[Institute of Systems Biology]] | :[[Institute of Systems Biology]] | ||
| + | ;Class | ||
| + | :{{Class|biouml.plugins.modelreduction.StoichiometricAnalysis}} | ||
;Plugin | ;Plugin | ||
| − | :biouml.plugins.modelreduction (Model reduction plug-in) | + | :[[Biouml.plugins.modelreduction (plugin)|biouml.plugins.modelreduction (Model reduction plug-in)]] |
==== Description ==== | ==== Description ==== | ||
| Line 11: | Line 13: | ||
If a reaction network has ''n'' reactions and ''m'' participating molecular species then the dynamic mass balance equation can be written as | If a reaction network has ''n'' reactions and ''m'' participating molecular species then the dynamic mass balance equation can be written as | ||
| − | :: [[File: | + | :: [[File:Differential-algebraic-equations-Stoichiometric-Matrix-stoich1.png]] |
where ''v'' is the flux vector and ''S'' is the concentration vector: | where ''v'' is the flux vector and ''S'' is the concentration vector: | ||
| − | :: [[File: | + | :: [[File:Differential-algebraic-equations-Stoichiometric-Matrix-stoich2.png]] |
==== Example ==== | ==== Example ==== | ||
| Line 21: | Line 23: | ||
Consider the following system of reactions: | Consider the following system of reactions: | ||
| − | :: [[File: | + | :: [[File:Differential-algebraic-equations-Stoichiometric-Matrix-stoich3.png]] |
This systems comprises four reactions and five different molecular species. The stoichiometry matrix for this system can be written as: | This systems comprises four reactions and five different molecular species. The stoichiometry matrix for this system can be written as: | ||
| − | :: [[File: | + | :: [[File:Differential-algebraic-equations-Stoichiometric-Matrix-stoich4.png]] |
where the rows correspond to ''S''<sub>1</sub>, ''S''<sub>2</sub>, ''S''<sub>3</sub>, ''S''<sub>4</sub> and ''S''<sub>5</sub>, respectively. Note that the process of converting a reaction scheme into a stoichiometry matrix can be a lossy transformation, for example, the stoichiometries in the second reaction simplify when included in the matrix. | where the rows correspond to ''S''<sub>1</sub>, ''S''<sub>2</sub>, ''S''<sub>3</sub>, ''S''<sub>4</sub> and ''S''<sub>5</sub>, respectively. Note that the process of converting a reaction scheme into a stoichiometry matrix can be a lossy transformation, for example, the stoichiometries in the second reaction simplify when included in the matrix. | ||
[[Category:Analyses]] | [[Category:Analyses]] | ||
| − | [[Category: | + | [[Category:Differential algebraic equations (analyses group)]] |
[[Category:ISB analyses]] | [[Category:ISB analyses]] | ||
[[Category:Autogenerated pages]] | [[Category:Autogenerated pages]] | ||
Latest revision as of 18:14, 9 December 2020
- Analysis title
 Stoichiometric Matrix
Stoichiometric Matrix
- Provider
- Institute of Systems Biology
- Class
StoichiometricAnalysis- Plugin
- biouml.plugins.modelreduction (Model reduction plug-in)
[edit] Description
The stoichiometric matrix N provides the linear relationship of the model between the flux rates of the (enzymatic) reactions and the derivatives of the reactant (enzyme) concentrations.
If a reaction network has n reactions and m participating molecular species then the dynamic mass balance equation can be written as
where v is the flux vector and S is the concentration vector:
[edit] Example
Consider the following system of reactions:
This systems comprises four reactions and five different molecular species. The stoichiometry matrix for this system can be written as:
where the rows correspond to S1, S2, S3, S4 and S5, respectively. Note that the process of converting a reaction scheme into a stoichiometry matrix can be a lossy transformation, for example, the stoichiometries in the second reaction simplify when included in the matrix.