Difference between revisions of "1-dimensional arterial tree model"
From BioUML platform
Tagir Valeev (Talk | contribs) (DOI) |
|||
| Line 1: | Line 1: | ||
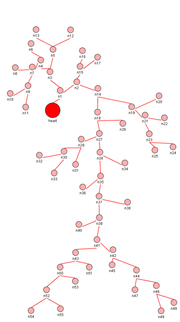
[[File:arterial.png|thumb|Arterial tree model]] | [[File:arterial.png|thumb|Arterial tree model]] | ||
| − | The 1D hemodynamic model of the human arterial tree, comprising 55 largest arteries, was obtained from Navier-Stokes equations after integrating them over arbitrary axial section<ref>Lamponi D.N. One dimensional and multiscale models for blood flow circulation. Lausanne, EPFL, 2004.</ref>. The boundary conditions for this system at each bifurcation point of the arterial tree were specified using the mass and energy conservation laws. A special tree packing algorithm and a numerical calculation method for this model were proposed. After time-discretization, the boundary value problem for a system of 110 ordinary differential equations was obtained at each time layer. The system is solved with the help of the orthogonal sweep method. | + | The 1D hemodynamic model of the human arterial tree, comprising 55 largest arteries, was obtained from Navier-Stokes equations after integrating them over arbitrary axial section<ref>Lamponi D.N. One dimensional and multiscale models for blood flow circulation. Lausanne, EPFL, 2004. {{doi|10.5075/epfl-thesis-3006}}</ref>. The boundary conditions for this system at each bifurcation point of the arterial tree were specified using the mass and energy conservation laws. A special tree packing algorithm and a numerical calculation method for this model were proposed. After time-discretization, the boundary value problem for a system of 110 ordinary differential equations was obtained at each time layer. The system is solved with the help of the orthogonal sweep method. |
==References== | ==References== | ||
Latest revision as of 11:42, 1 July 2013
The 1D hemodynamic model of the human arterial tree, comprising 55 largest arteries, was obtained from Navier-Stokes equations after integrating them over arbitrary axial section[1]. The boundary conditions for this system at each bifurcation point of the arterial tree were specified using the mass and energy conservation laws. A special tree packing algorithm and a numerical calculation method for this model were proposed. After time-discretization, the boundary value problem for a system of 110 ordinary differential equations was obtained at each time layer. The system is solved with the help of the orthogonal sweep method.
[edit] References
- ↑ Lamponi D.N. One dimensional and multiscale models for blood flow circulation. Lausanne, EPFL, 2004. doi:10.5075/epfl-thesis-3006